על קיבועים ודרגות חופש באנליזת חוזק
אם גם לכם יצא לשאול או לומר: "האם האנליזה שלי מדויקת?" , "בניסוי הפיזי זה מתנהג אחרת לגמרי!" , "סימולציות זה נחמד, אבל הרבה פעמים זה מחזיר שטויות" – אז המאמר הבא הוא לגמרי בשבילכם.
אז "האם האנליזה שלי מדויקת?" – אולי..
ומה עם "בניסוי הפיזי זה מתנהג אחרת לגמרי!" – כנראה.
ולא תכחישו ש- "סימולציות זה נחמד, אבל הרבה פעמים זה מחזיר שטויות" – ללא ספק!
מבולבלים? עד סוף המאמר כבר לא תהיו.
הגדרת תנאי הגבול באנליזה, באופן שישקף בצורה המיטבית את המציאות האמיתית, הינה מיומנות חשובה מאוד (שלא לומר אומנות) למתכננים מכאניים המבצעים סימולציות.
למרות שמה שמתקשר לנו אינסטנקטיבית כשאנחנו מדברים על "דיוק" הוא – איכות הרישות, אפשר להשקיע המון זמן בהגדרת הרישות המושלם למודל ועדין לקבל תוצאות מופרכות שלא קשורות למה שעתיד לקרות במציאות.
מאמר זה עוסק באחד הגורמים המשפיעים ביותר על נכונות ודיוק תוצאות האנליזה והוא: אופן הריתום של המודל במרחב.
וכדי להבין לעומק את נושא הריתום, חשוב להיסגר קודם על המושג שנקרא "דרגות חופש".
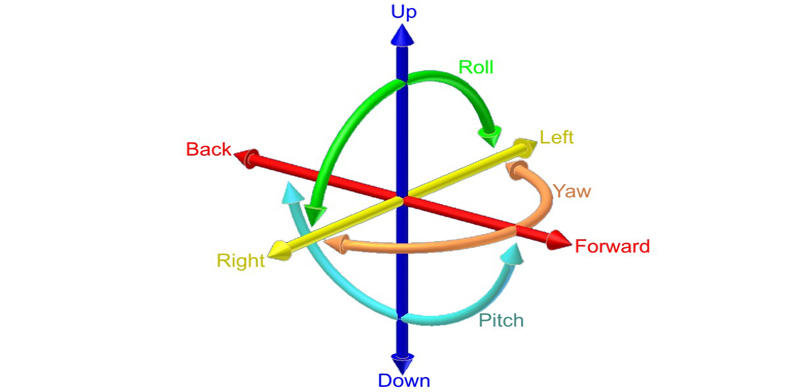
באנליזת חוזק, דרגות חופש הן למעשה היכולת של כל ישות במודל (פאה, קו גוף ואפילו נקודה) לנוע בכל אחד מששת הכיוונים הבאים, ביחס לעצמה.
בכל פעם שאנחנו מגדירים ריתומים (Fixtures) באנליזה, אנו למעשה מגבילים דרגות חופש של ישויות נבחרות במודל, כלומר: מקבעים אותו בכיוונים שאנו חושבים שלא יזוז במציאות.
וכשמה שאנחנו מגדירים (או מניחים) לא דומה למציאות – התוצאות בהתאם.
אז כדי להפנים את החשיבות, ללמוד איך להגדיר נכון ריתומים ולא פחות חשוב – איך להימנע מטעויות, נבחן את הבעיה (הקלאסית) הבאה:
נעשה זאת על ידי בחינת אותה הבעיה במספר דרכי ריתום שונות, ונשווה בינהן.
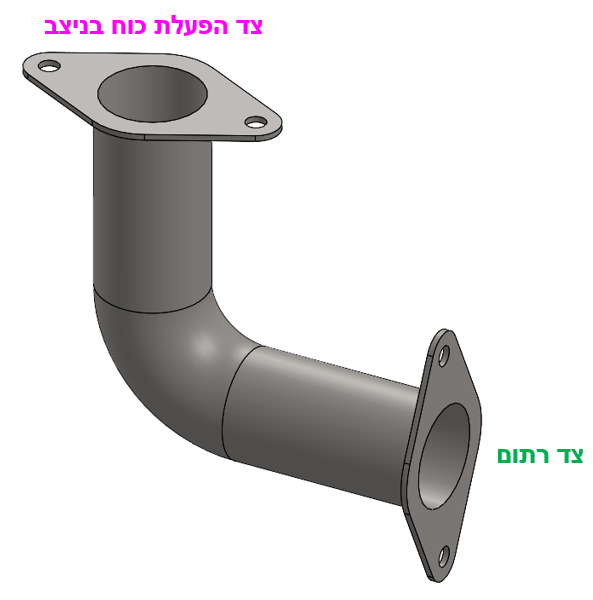
במציאות: הצינור הזוויתי רתום לקיר בשני ברגים העוברים דרך הפלאנג'.
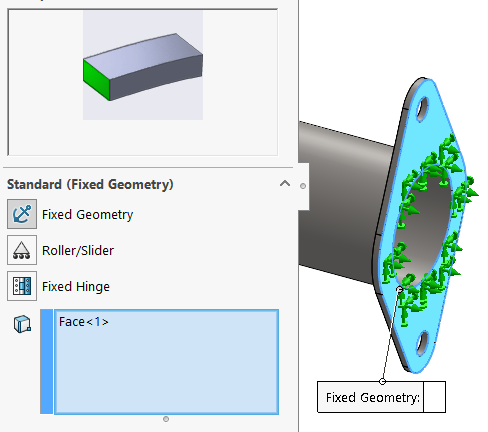
Fixed Geometry
אופן ההגדרה:
משמעות: קיבוע אבסולוטי של כל הפלאנג', הפאה מקבלת קשיחות אינסופית ואינה יכולה להתעוות.
מספר דרגות חופש מוגבלות: 6 (כולן)
יתרון: הגדרה קלה, זמן פתרון מהיר.
חיסרון: מצב שכמעט ולא מתקיים במציאות.
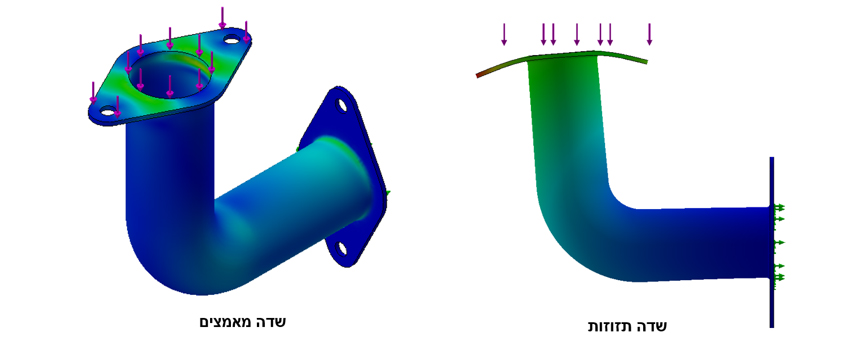
ניתוח תוצאות:
הפלאנג' ישר לגמרי, ללא תזוזות וללא מאמצים. ההקשחה של הפלאנג' גורמת לכוח הפועל לרכז את האנרגיה בפלאנג' השני (העליון) ולקפל אותו כלפי מטה.
מסקנה: הציפייה לריכוז מאמצים באזור הרתום לא התממשה. מכאן שהמצב אינו מציאותי כלל.
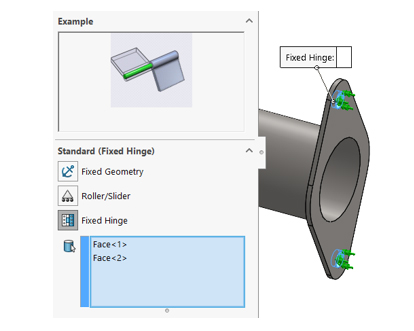
Fixed Hinges
אופן ההגדרה:
משמעות: קיבוע צירי של פאות הקדחים בפלאנג'.
מספר דרגות חופש מוגבלות: 5. מתאפשרת רוטציה סביב ציר המרכז של כל אחד מהקדחים בלבד.
יתרון: הגדרה קלה ומציאותית יותר מ-Fixed על אותן פאות. זמן פתרון מהיר.
חיסרון: בגלל קיבוע דרגות החופש בכיוון הרדיאלי, פאות הקדחים אינן יכולות להתעוות ולכן מרכזות אליהן מאמצים גבוהים מהמציאות
ניתוח תוצאות:
רוב המאמצים מתרכזים באזור הרתום וזה עולה בקנה אחד עם הציפייה. למרות זאת, הפלאנג' מתעוות פנימה משום שאין "קיר" שיגביל אותו, מה שככל הנראה גורם לריכוז מאמצים גבוה מידי בחלק התחתון של הפלאנג'.
מסקנה: תוצאות סבירות יחסית להשקעה מינימלית בהגדרת ריתום, אך עדין לא משקפות היטב את המציאות.
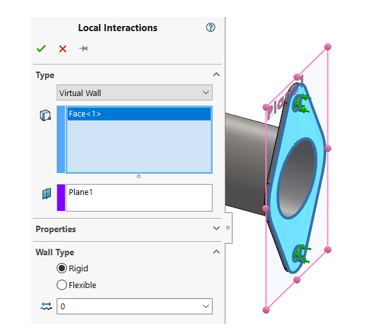
Virtual Wall + Fixed Hinges
אופן ההגדרה:
משמעות: הגדרת קיר וירטואלי כנגד הפלאנג'. ההגדרה מתאפשרת דרך תפריט Local Interactions.
מספר דרגות חופש מוגבלות: 5 – בפאות הקדחים. חשוב להבין ששטח הפלאנג' שנוגע בקיר אינו מוגבל בדרגות החופש, אלא רק בתנועה כלפי הקיר. הפלאנג' יכול להתנתק מהקיר אבל לא לחדור אותו.
יתרון: הקיר הוירטואלי מדמה טוב יותר את המציאות כיוון שמתנהג כגורם חיצוני ולא כריתום במודל.
חיסרון: אותו חיסרון שבשימוש ב- Fixed Hinge. בנוסף, הקיר הוירטואלי מאריך את זמן הריצה של הפותרן.
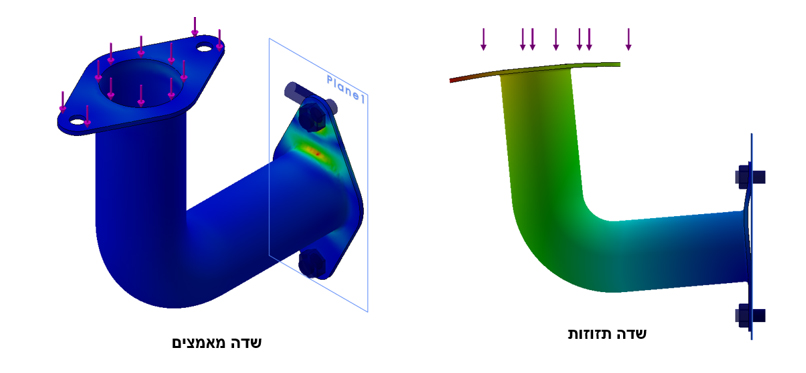
ניתוח תוצאות:
מסקנות:
הפלאנג' מתעוות בדומה לאינטואיציה – מתיחה משמעותית בחלקו העליון וכיווץ מתון בחלקו התחתון. הגדרת הקיר הוירטואלי הוכחה כקריטית לבעיה זו והמבחן מקבל ציון "עובר".
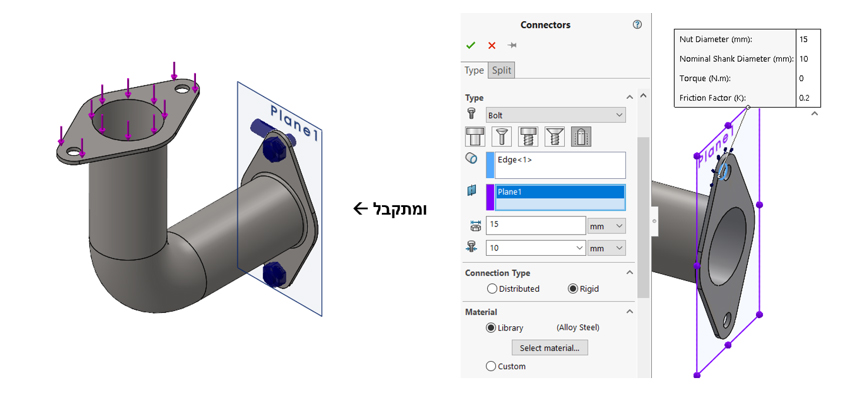
Virtual Wall + Foundation Bolts
אופן ההגדרה:
משמעות: הגדרת קיר וירטואלי וברגים וירטואליים המחברים את הפלאנג' אליו.
מספר דרגות חופש מוגבלות: אין מגבלה של דרגות חופש משום שאין קיבועים, רק אלמנטים וירטואליים שדופנים את המודל.
יתרון: הגדרה מציאותית לחלוטין.
חיסרון: האלמנטים הוירטואליים (קיר וברגים) מאריכים את זמן הריצה של הפותרן. כמו כן הגדרת הברגים מצריכה השקעה רבה יותר ביחס לשימוש בקיבועים (Fixtures).
תוצאות:
עיוות הפלאנג' תואם במדויק למציאות. ניתן לראות החמרה של ריכוז המאמצים באזור המתיחה ביחס למבחן הקודם.
מסקנה: למרות הדמיון למבחן הקודם, הגדרת הקיר עם הברגים היא ההגדרה המציאותית ביותר ועל כן תחזיר את הערך המספרי המדויק ביותר.
לפני סיום, ניואנס נוסף:
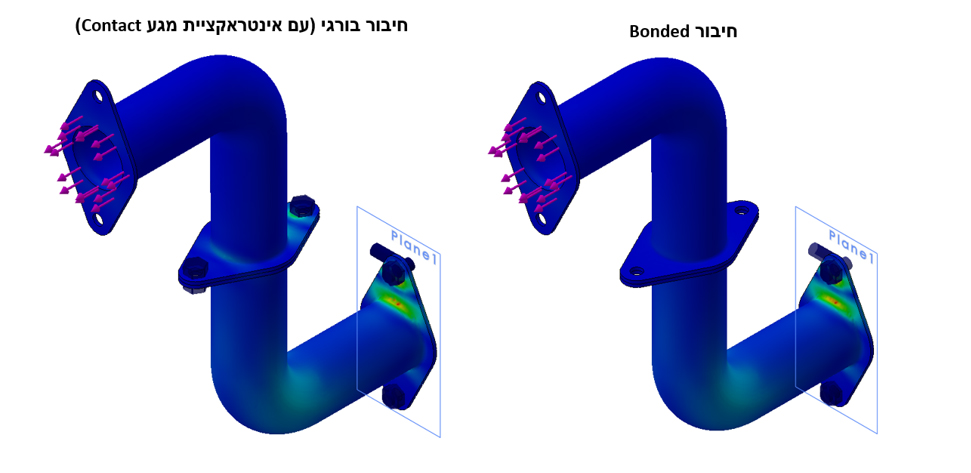
Bolt Connector VS Bonded Interaction
מצב של "קיבוע ייתר" עלול לקרות לא רק בריתום והגבלת דרגות חופש של יישויות במודל, אלא גם באינטראקציה (מגע) בין חלקים (באנליזה על חלק מרובה גופים או הרכבה).
נראה זאת בהשוואה הבאה, בה נבחן מצב של חיבור בורגי בין שני פלאנג'ים לעומת הגדרת אינטראקציית Bonded בינהם:
בחינת אזור הממשק בין הפלאנג'ים לא משאירה מקום לספק – חיבור בורגי במקרה שכזה הוא קריטי לנכונות פתרון האנליזה.
לסיום,
מי מכם שמתלבט בנוגע להגדרת קיבועים באנליזה ספציפית או שמעוניין בפרטים נוספים כמו איזה אפשרויות קיימות בהגדרת ברגים, מה עושים במצב של קיר גמיש, האם התוצאות שקיבלתי נכונות או רחוקות מהמציאות ועוד.. צוות הסימולציות זמין לשירותכם בתמיכת SOLIDWORKS בסיסטמטיקס.